自然界中充滿了自我相似的特性，而這些特性十分適合數學和電腦中的迭代，今天就讓我們一窺L系統（Lindenmayer Systems）的奧秘。

L系統（Lindenmayer Systems）

L系統是由匈牙利生物學家Lindenmayer在建構酵母和菌類形態的數學時建立，希望能提供一種正式的模型來描述一些簡單多細胞的生物發展情況，後來這個模型也擴大來描述高等植物的生長形態。

L系統的結構定義為數對

• V：符號集合，包含迭代後會改變的符號（變數，Variable）和不會改變的符號（常數，Constant）。
• ：由Ｖ的元素構成的起始符號串，稱之為axiom、start或initiator。
• P：迭代規則集合，Production rules，例如A->BA代表迭代時，A會被AB代替。若V裏面的元素沒有出現在P所有規則的箭頭左邊，則視為常數，迭代時，保持原符號。

L系統範例Algae：

• variable：A，B
• axiom：A
• rules：(A->AB)，(B->A)
• 第一次迭代結果：AB
• 第二次迭代結果：ABA
• 第三次迭代結果：ABAAB
• 依此類推…

目前較常用字元的意義：

• F：向前移動並畫一個線段。
• f：向前移動但並不畫線。
• +：逆時針旋轉一個角度。
• -：順時針旋轉一個角度。
• |：反向180度。
• [：開始分支，儲存進入分支的方向和位置。
• ]：結束分支，恢復進入分支的方向和位置。

JSXGraph實作

JSXGraph官網的範例中，提供了L系統的實作程式碼如下：

function expander(level, axiom, rules) {
  this.axiom = axiom;
  this.rules = rules;
  this.source = (level > 1) ? new expander(level - 1, axiom, rules) : (new function() {
    // Axiom:
    this.code = axiom;
    this.pos = 0;
    this.next = function() {
      if (this.pos >= this.code.length) return null;
      return this.code.charAt(this.pos++);
    }
  });

  this.code = '';
  this.pos = 0;
  this.next = function() {
    while (this.pos >= this.code.length) { // produce new symbols from source
      this.pos = 0;
      let pattern = this.source.next();
      if (!pattern) return null // Finished
      this.code = this.rules[pattern];
    }
    return this.code.charAt(this.pos++);
  }
}
async function plotter(generator, symbols, len, angle, t, shrink) {
  for (let c; c = generator.next(); c) {
    console.log(c)
    switch (symbols[c]) {
      case 'F':
        t.fd(len);
        break;
      case 'f':
        t.penUp();
        t.fd(len);
        t.penDown();
        break;
      case '+':
        t.lt(angle);
        break;
      case '-':
        t.rt(angle);
        break;
      case '[':
        t.pushTurtle();
        len *= shrink;
        break;
      case ']':
        t.popTurtle();
        len /= shrink;
        break;
      default:
        ;
    }
    await sleep(10)
  }
  return null;
}

function sleep(millisecond) {
  return new Promise(resolve => {
    setTimeout(() => {
      resolve()
    }, millisecond)
  })
}

為了方便觀察畫線的步驟，我加上了昨天的sleep函式。
下面是level=5的Koch曲線執行結果。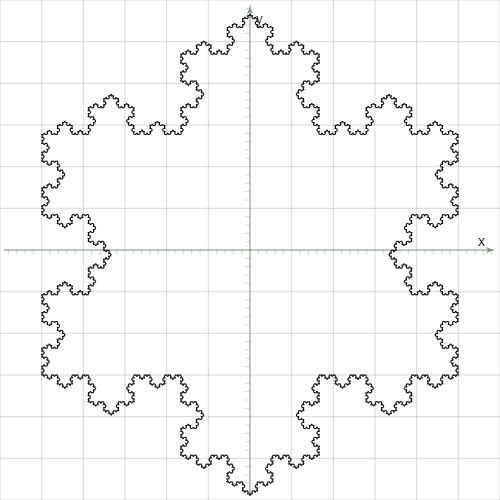

參考資料

• 維基百科：https://en.wikipedia.org/wiki/L-system
• 兔子與L-System：https://prototypingideas.blogspot.com/2012/12/l-system.html
• JSXGraph官網範例：https://jsxgraph.uni-bayreuth.de/wiki/index.php/L-systems

程式原始碼

今日程式原始碼
今天的程式，由於時間的關係，介面部分沒有好好處理，待鐵人賽結束後，再回過頭來進行加強。有興趣的朋友，可以試著將維基百科範例，在程式中實作，看看是否能跑出一樣的圖形。

今日小結

很久以前在一次研習的時候，看到交通大學陳明璋老師用自己開發的Powerpoint巨集進行山水畫創作，甚感驚訝，但是並沒有跟進深入了解；沒想到這次鐵人賽的機會，花了一天的時間，總算稍稍了解L-System。在兔子與L-System中有建議Lindenmayer合著的經典著作 The Algorithmic Beauty of Plants，有時間要好好的閱讀一番。鐵人賽已經接近尾聲，希望自己能撐過最後三天，加油！